第十章 变成高手最快只需要一年的时间¶
当然,读者看到这裡还是会有点担心。我前面教的好像只是短期的速学法。非也,我只是透过一些数学手段计算
- 让一些我们原本用感觉去量测的目标,变得清晰可见
- 设立目标就不容易订歪。不然常常自己只是要解新手问题,结果在整个高手问题森林迷路了。
- 再来就是因为有具体方向了,也有题目的数量了。所以整个学习过程变成有进度条,辛苦也会渐渐能够忍受了。因为你是能够看得到终点的。
但回归到一个现实问题,我们有时候不只是想短期的学技术。我们更多时候,是要进行长期领域的攻克。那麽针对这个方向,我们要如何进行攻克?
德雷福斯模型:专家、精通者、胜任者、高级新手、新手¶
关于长期领域的攻克进度,业界有一个具体的模型:德雷福斯模型(Dreyfus model of skill acquisition),这个模型将技能熟练度,由上而下分成:专家,精通者,胜任者,高级新手,新手五个等级。
在攻克一个领域的过程中,可以将能力值分为五个阶段:
- 新手
- 高级新手
- 胜任者
- 精通者
- 大神
每个领域都有相对明确的 KPI。前面我在新手老师设计课程的盲区这一块提过,并没有将自己的能力 1 * / 10 的这种事。是因为能力分级只有五级。而每一层需要到达的水准、练习方向、准备方式完全不一样。而每一层需要的知识更是指数型成长,所以不可能存在教 1/10 的大师所知道的知识就可以把你教会。
那麽,我们在每一阶段,通常需要多少练功时长呢?
你可能会以为这是没有办法被进行估算的。
以工程师这一行来说的话,其实已经有相对贴近事实的时间统计了。
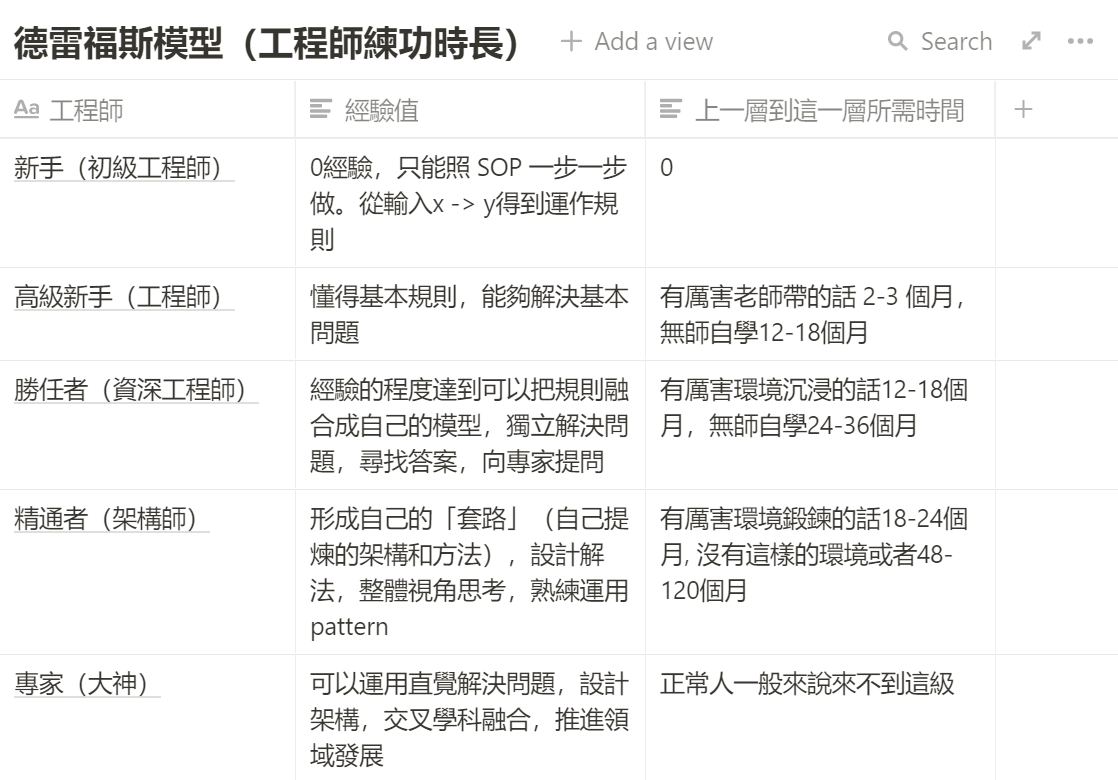
- 高级新手从 2-3 个月到12-18个月不等(有无厉害老师带练)
- 胜任者从12-18个月到24-36个月不等(有无厉害环境沉浸)
- 精通者从18-24个月到48-120个月(有无环境发挥锻鍊)
- 专家则靠机遇
其实这个模型列出的估算时间,不只是适用在工程师这一行。大多领域也是这个大概的时间范围。
而所需要的时长,端看你想攻克到哪一些阶段,以及中间有没有找到厉害的老师帮你缩短时间。
而且,你可能更听说过一件事,如果你已经到达一个领域的精通者或大神级别,通常你再攻克另外一个领域的时间,会指数型下降。精通更多领域,学一门新学问的所需时间会大幅减少。
所以你真的不需要一万小时才能够学会一门技能。通常我们所说的“会”,顶多就是高级新手、胜任者阶段而已。按照这个标准,快的话两三个月,慢的话顶多一年多。
你可能会觉得这个数字不可能这麽短吧。
事实上是可能的,因为公司的训练教育就是如此阿,公司是要赚钱的,不是找一个人来当学生学生慢慢学的。
公司的工作训练基本上就是前辈带后辈,先教怎麽做(程序性知识),然后再慢慢补充细节(事实性以及概念知识),透过每天解决不同的业务问题以及发问,得到快速成长的结果。
如果一个公司还让你从基础知识学起的话,那这间公司也老早就倒了。
鬼速学习法 — 如何将无限的学习旅程压缩到光速学会¶
再来,以我本人的经历。甚至觉得上面这个表所写的这个数字还太高了。这是一般人学习时,所需要的“自然”时间。
自然是指碰运气看书、碰运气找老师、碰运气找到有系统训练的公司、够多机会可以历练。也就是题目出现的机率是自然的,解题出现的机率是自然的,你只是等在那裡,被动的被系统 assign 学习的机器。
但如果我们主动呢?
让我提出一个你从来没想过的角度吧。
为什麽我们常会觉得学习是无限的?
这是因为往往我们在遇到一个新问题点时,为了解决这个问题,我们可能突然间又会遇到 3-5 个子问题。为了解决这当中的子问题,每一个子问题,我们又会再遇到 3-5 个孙问题。
接著。。。。。就没有接著了,你会觉得这没完没了,就直接放弃了。
因为你不知道到底后面会有多少问题,自己还要花多少时间呢?
让我问你一个问题,如果你认真挖下去,一直挖到最底层不会产生新的子问题,那麽所有的问题加起来要花多少时间。你可能从来没有想过这件事吧?
而这个问题其实是有答案的。
我们人类之所有会对无穷无尽的问题放弃,是因为我我们人类的短时记忆区只能容纳 3-5个子主题。这是我们对一个问题瞬时间所容忍的数学极限。所以当 1 个问题,膨胀到 9-25 个问题时,我们立刻就会崩溃。自然就会算了。。。。
但是若我们反过来想这件事呢?
前面我写到,我们在学习时,可以反过来学习,抱怨自己遇到的问题。其实整理下来,可能就只有大约 9-25 个问题而已。然后其实这九个问题又可以被分类到 3-5 大类。
事实上,我认为几乎世界上所有的问题、答案基本上都是 3 次方的,而他们是以这样的结构存在
- 1,2,3
- 前,中,后
- 输入,处理,输出
- 是什麽,为什麽,如何做
又或者是各种领域自己的结构
- (学习) - 目标、过程、如何持续
- (做生意) - 招客、服务、成长
- (剖析财报) - 利润率,总资产週转率,槓杆倍数
好。假设遇到的问题。我们都可以用以上的步骤,从终点用“三部曲”拆解。然后拆到没有颗粒为止。
那我们总共要解决多少个问题呢?我们可以先穷尽一下问题的数量,试著把3的次方都算出可能性。
- 3**4 = 81
- 3**5 = 243
- 3**6 = 729
- 3**7 = 2187
- 3**8 = 6151
假设我们解决一个问题要 1 天
那麽可能就需要:
- 90 天
- 8个月
- 2 年
- 5 年
- 16 年
事实上你会发现这几乎就近似于成为(野生)高级新手,胜任者,精通者,专家需要的时间。
如果再让你重新回来看到这个表,你会不会发现什麽微妙之处了呢?

但多数市面上只要达到胜任者、精通者,大家就会认为他是专家了。而且,更多时候,你只要达到高级新手,人家(完全不懂的人)就会认为你是专家了。
而解决问题需要一天的时间。这是抓比较宽鬆的。
假设我们如果解一个问题是 8 小时,也就是只需要原来 ⅓ 的时间。(假设我们用机器或框架求解)
那麽所需时长就会变成
- 30 天
- 90 天
- 8个月
- 2 年
- 5 年
而这个数字,贴近于(幸运有环境)的高级新手,胜任者,精通者,专家需要的时间。
当然我们也可以再短下去。假设一个问题只要再 ⅓ 也就是 2.6 小时
那就会变成是:
- 10 天
- 30 天
- 90 天
- 8个月
- 2 年
事实上我现在学习一个新领域的耗时程度,差不多也是如此。
- 到胜任者的时间只需 90 天
- 到精通者的时间 8 个月
- 到专家的程度 2 年内
当然,我写这本书的目的不是要吹嘘我自己学习速度有多夸张。而是要让各位读者同样也拥有相同的能力。我只是利用数学模型去展示,这是完全有可能的一个理论。
光速学习能力的时间与成本¶
如何才能做到如此变态的学习速度呢?
刚刚我们谈完了问题极限,列出了3的次方可能性:
- 3**4 = 81
- 3**5 = 243
- 3**6 = 729
- 3**7 = 2187
- 3**8 = 6151
但事实上我不认为一个领域可以要研究到 6151 个问题。大概 2187 个问题就差不多了。
所以要解的就是
- 81 高级新手
- 243 熟练者
- 729 精通者
- 2187 专家
假设高级新手有 81 个问题。一本书能解你 3 个问题。你其实需要 27 本书。
以此类推,所以你需要
- 27 本书
- 81 本书
- 243 本书
- 729 本书
事实上一个领域买到 729 本书也不太可能。243 是比较有可能的数字。因为同一个领域,许多书的内容都有一定程度的重複。我当时为了学习财报分析买了四百本书,后来大致翻完,我感觉读起来像是 81 本不同书而已。
而刚刚我们说到:假设高级新手有 81 个问题。按照一本书能解你 3 个问题。你其实需要 27 本书。
(你不需要把整本书读完,只要那本书能够解你一个子问题或孙问题就够了,实际点!)
一本书 300 块。27 本书就是 8100 块。解决一个问题成本100块。
你看 27 本书。假设 1 本书需要看 1 天。那就是 27 天可以看完(+练完)变成高级新手。
30 天高级新手不是什麽不可能的事。那熟练者 90 天也是可以做到的事。
而且,看书还是比较慢的方法。通常我会去上课。有些领域理论上我自学 30 天应该也有办法学到高级新手。但是去上高手开的课,可能 1 天花 8100 块以内就学会。但是时间上我只需要花 1 天,而不是 30 天。
所以好课与烂课其实是能不能将原先 30 天练功时间缩到 1 天,节省 30 倍时间。而不是上完课之后,不仅成果为 0 ,甚至反而更打击自己的自信心。
这样算下来,你还会觉得学习、锻鍊的目标还是看起很远吗?